Analytic Expressions for Probabilistic Moments of PL-DNN with Gaussian Input

Abstract

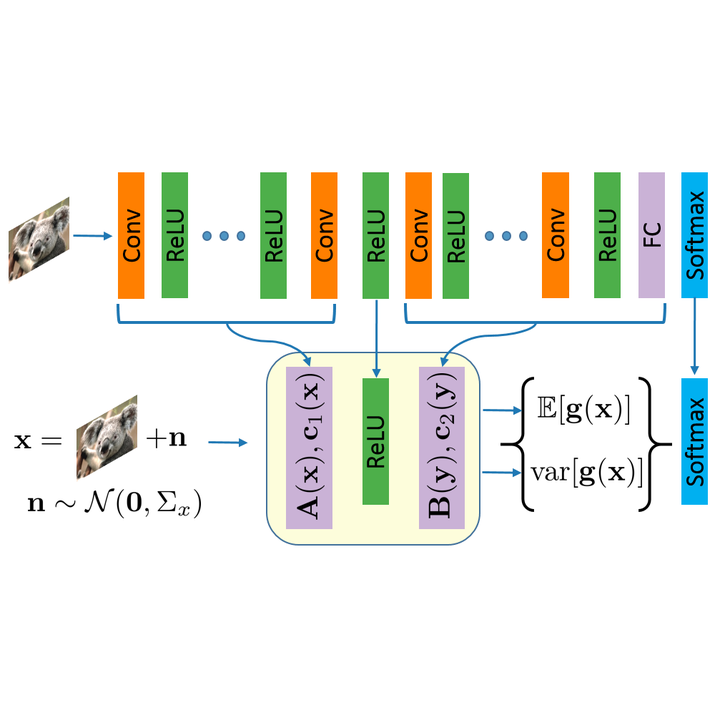
The outstanding performance of deep neural networks (DNNs), for the visual recognition task in particular, has been demonstrated on several large-scale benchmarks. This performance has immensely strengthened the line of research that aims to understand and analyze the driving reasons behind the effectiveness of these networks. One important aspect of this analysis has recently gained much attention, namely the reaction of a DNN to noisy input. This has spawned research on developing adversarial input attacks as well as training strategies that make DNNs more robust against these attacks. To this end, we derive in this paper exact analytic expressions for the first and second moments (mean and variance) of a small piecewise linear (PL) network (Affine, ReLU, Affine) subject to general Gaussian input. We experimentally show that these expressions are tight under simple linearizations of deeper PL-DNNs, especially popular architectures in the literature (e.g. LeNet and AlexNet). Extensive experiments on image classification show that these expressions can be used to study the behaviour of the output mean of the logits for each class, the interclass confusion and the pixel-level spatial noise sensitivity of the network. Moreover, we show how these expressions can be used to systematically construct targeted and non-targeted adversarial attacks.